3 Offbeat South 4 Puzzles
The final rounds of a mahjong game often contain the most interesting decisions.
In the east round of an east-south mahjong game, we play relatively straightforward, balancing the reward of winning our hand with the risk of dealing in to an opponent’s hand. On ladder, where only placement affects the payouts of the game, the final round can encourage some more polarized strategies. We may want to feed a player’s hand to protect a first place. We may want to hold back tiles to avoid feeding a competitor. We may need to meet a certain point requirement to escape 4th place, forcing us to build for value. Understanding each player’s incentives should influence our strategy.
The final round also has the most consequential decisions.
In this post, we’ll assume a normalized reward system of [2, 1, 0, -3] for 1st through 4th place. While a mangan win in East 1 moves our expected reward by around 1 point, it could be a swing from 4th (-3 pts) to 2nd place (-1 pt) for 4 pts in all last.
I want to share 3 of the most interesting South 4 decisions I’ve come across in my last 400 games of mahjong. Can you find the most optimal moves in the most important round of the game? I encourage readers to make their decision with reasoning before reading my analysis. For an additional challenge, come up with your gut answer (you only get 5 seconds + your time bank in a real game), and your thought out answer.
Calls: chii => south, chii => 2p
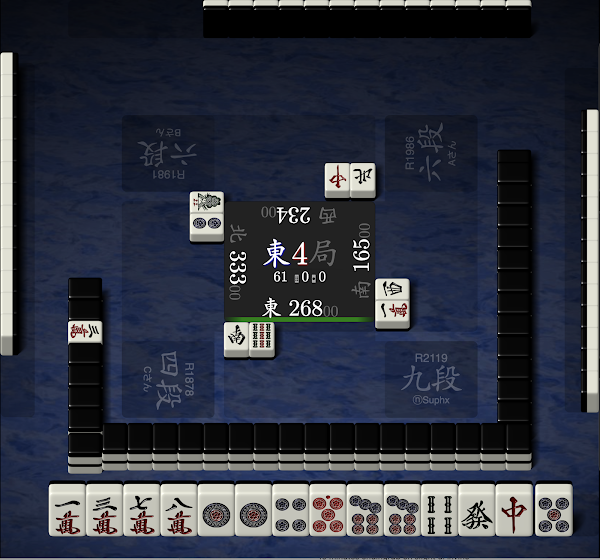
Tiles cut from the hand are white, and tiles that were cut upon being drawn are gray.
The number 9 in the center of the board shows how many tiles are left to be drawn in the round. On the last draw of the round, there will be 0 draws remaining.
Let’s start by ignoring the irrelevant players. 1st place is dealer in South 4 with a big lead, so they will simply fold and confirm 1st. 2nd place has a sizable lead over 3rd and 4th, with no incentive to take any risk with 2 draws left, so they will also fold. We can confirm from their last several safe discards from hand that they are choosing to fold.
We’re in 3rd place at 1-shanten, with a small lead over 4th. If we can hit tenpai within our final 2 draws, we can confirm 3rd place on exhaustive draw. 4th place has 3 draws, and can escape 4th by winning a hand, or hitting tenpai, while 3rd place misses out on tenpai.
I ran the hand in the pystyle simulator. The left column shows the types and number of tiles we accept to hit tenpai, which ranges from 13-16 depending on our choice. The rightmost column shows an estimate of how often we hit tenpai, which ranges from 20.9-25%.
Pystyle does not consider making calls from other players which is fine, since we do not expect to get fed by 2nd place, who is folding. We could potentially call pon on a tile 4th place cuts, but we’ll ignore this minor detail in our analysis.
My initial reaction to this problem was to cut 5s for maximum tile acceptance, but there is a tradeoff. If we cut 5s, we might feed 4th place a call into tenpai, which would cost us if they hit tenpai while we don’t. How do we know if this tradeoff is worth it?
Let’s try to make a read on how far 4th place is from tenpai. In row 2, they cut the 13m kanchan which was missing 2 tiles. Usually block cuts are done from 1-shanten or 2-shanten, but since the middle tiles 4p and 7m are in their discards, I would guess they were more likely 1-shanten. They cut 1s from their hand after. Since this was the last 1s, we can narrow down why they kept 1s in their hand. They could have done a slide - having 123s, and drawing 4s. They also could have upgraded or completed a shape. For upgrades, they could have 12s => draw 2s or 4s, or 13s => draw 3s or 4s. For block completions, they could have 122s or 133s => draw 2s or 3s. It seems like there are more scenarios where 4th place did not advance from 2-shanten to 1-shanten, or 1-shanten to tenpai.
And most importantly, they haven’t declared riichi. We would expect 4th place to declare riichi unless they had a yaku to be able to declare ron. Usually this would be pinfu or tanyao, but pinfu is impossible if they completed 122s or 133s by drawing 2s or 3s. We can also rule out completed yakuhai as a yaku, and seven pairs is unlikely because of how long the dead 1s was held.
I’ll give 4th place a 10% chance of being tenpai, a 65% chance of being 1-shanten, and a 25% chance of being 2-shanten.
If 4th place is 1-shanten, what is the chance that each tile feeds them into tenpai, costing us our position?
With 4 4p and 4 8p visible, a row 1 49p cut, and 1 7p visible, 57p will pretty much never feed 4th place a call. With 5s and 6s, we could estimate the feed chance by the dealin rate of these tiles vs a riichi. Presumably 4th place is 1-shanten with one incomplete block around 1s and one elsewhere, so this should be a decent estimate. Consulting a dealinrate chart, non suji 56 is around 21% dealinrate on Turn 16. 6s is one chance on one side, making it less likely to feed than 5s. We could make a lower bound estimate of its dealinrate to be around 16%.
Finally, let’s estimate 4th place’s chance of hitting tenpai with 3 draws left. If they have a 16 tile 1-shanten, they hit tenpai roughly 35% of the time according to pystyle.
With all of these numbers, we can come to an estimate of the chance we get 4th place. We’ll ignore the 2-shanten case for simplicity, and assume that neither us nor 4th place wins the hand before exhaustive draw. These assumptions will not affect the results much, since with 2 or 3 draws, it is very rare for a 1-shanten hand to win or a 2-shanten hand to hit tenpai. We’ll also see from the results that the difference between the decisions is large enough that we don’t need a more precise analysis.
P(we get 4th) ~= P(we are not tenpai) * [P(4th place is tenpai) + P(4th place is 1-shanten) * [P(4th place does not call our tile) * P(4th place gets tenpai by self draw) + P(4th place gets tenpai by calling our tile)]]
57p cut:
4th rate = (1 - .2094) * [.1 + .65 * .35] = 25.9%
5s cut:
4th rate = (1 - .2499) * [.1 + .65 * [(1-.21) * .35 + .21]] = 31.2%
6s cut:
4th rate = (1 - .2365) * [.1 + .65 * [(1-.16) * .35 + .16]] = 30.2%
Conclusion: we should cut 57p to avoid the chance we feed 4th place into tenpai. It’s not worth feeding 1-shanten => tenpai ~10-13% (16-21% feed * 65% 1-shanten) of the time for an additional 4% tenpai rate.
We want to maximize our chances of escaping 4th place, and any win will do. We should choose dama instead of riichi, keeping our chance of upgrading to a 3 sided wait. Should we wait on 1p or 9p?
Normally I would wait on the 9p, which seems more likely to come out due to the two 8p visible. However, Flan shared a problem on discord from a mahjong book by Kawamura Akihiro, which made me rethink this conventional wisdom.
In the book problem, we want to choose which ryanmen to break to maximize our winrate. We are given the information that the player on our left has cut 8m early. Most people want to keep the 78m block, hoping to catch 9m coming out.
The author argues that the other terminals 9p and 9s are more likely to come out. The left player is likely to cut 9p and 9s if they draw them, because terminals are generally hard to use (though 9m is harder to use). However, there is the added benefit that they might cut 9p or 9s from their hand, whereas 9m is likely not in their hand. In summary, a tile like 9p can be discarded after being drawn, or from the hand. 9m is slightly more likely to be discarded after being drawn, but less likely to be discarded from the hand.
The author refers to an analysis where 9m is cut in the early game 413 times, and the rest of the 5 terminals 2566 times. For a specific terminal, this is 2566/5 = 513.2 times. This is a 24% relative increase in the probability that the player cuts the other terminal in the early game, a pretty large difference.
I have some questions about this analysis, which was not fully detailed. What cutoff turn was used to define early game? What percentage of the time did our left player cut each terminal from hand, vs after drawing it? What percentage of the time are we able to draw the tile ourselves? If a tile we want to call is more likely to be in an opponent’s hand, it would also be less live in the wall, which may counteract the benefit of getting more calls. However, I do think that the analysis presented mitigates this downside. In the analysis described above, having the tile in the left player's hand is strong enough to make up for both the increased chance that they draw the tile (if it's not in their hand, it's more live in the wall), and the increased chance that they cut the tile after drawing it. And this increased chance is a suprising 24%. It seems plausible that we would rather have the tile in the left player’s hand than in the wall.
Let’s go back to the original problem. Our left player looks unlikely to have either 1p or 9p, and will probably cut both. The player across from us probably does not have 9p, but might have 1p, which according to the book significantly increases the chances that they feed 1p in an early turn. The player on the right may have both tiles, but are probably slightly more likely to have 1p, since 2 8p being visible makes them more encouraged to toss 9p. They’re probably slightly more likely to cut 9p if they draw it, but this may be balanced by the higher chance 1p is in their hand and will get cut. And finally, we have the counteracting effect of 9p being more live in the wall, making it more likely for us to draw it.
If you believe the logic from the book, the answer to this problem is probably that we should wait on 1p. Because of the book’s vague description of it's data collection process, I’m not fully convinced, but for now, I’ll tentatively say we should wait on 1p. I would like to see a replication of the book's findings in the future.
Here are the hands from that round:
Calls: pon => 9p, pon => white dragon
We have a honitsu hand that is tenpai, and we can escape 4th place by tsumo, or by ron on 2nd or 3rd place.
1st place is trying to feed our hand, since they can dealin to a 7 han hand and confirm 1st.
It looks like 2nd place has decided to fold, cutting a 1p from their hand, followed by 9m pair from their hand. Note that 2nd place has less of an incentive than 3rd place to fight. 2nd place can avoid 4th place by 100 pts if we mangan tsumo. Even if 2nd place folds, 3rd place might also fold allowing 2nd place to secure their position without taking any risk.
On the other hand, if 3rd place hits tenpai while 2nd place folds, they can steal 2nd place. 3rd place should be willing to take some risks for a chance at 2nd, keeping in mind the rewards of +1 for 2nd, +0 for 3rd, and -3 for 4th.
We have two options. We can call the north pair and go for furiten tsumo, or we can pass and go for tsumo or ron on 2nd / 3rd place. We probably won’t ron 2nd place, but 3rd place might cut north, or even 7s depending on the situation.
For example, on the last draw of the game if 2nd place had folded out, 3rd place should be willing to push up to a 25% dealin tile to go for 2nd place. 75% of the time, they would gain 1 pt, and 25% of the time they would lose 3 pts, for a net balance of 0 EV, making 25% the dealinrate threshold. North also seems decently safe, being a once cut honor tile if we pass this call. It’s possible 3rd place pushes north if they have a good wait tenpai, or are tenpai and we are close to exhaustive draw.
If we go for the furiten route, we would pon and cut 4s, giving a furiten wait of 4 tiles. North confirms our 4th han, so we don’t need the dora for points. We would upgrade from 3 to 4 outs, but we lose the ability to declare ron on 3rd place.
I think there are 2 factors that push this decision in favor of pon => cut 4s.
The first factor is the turn number. Normally, calling means you lose a draw, but this is not the case here, assuming no other calls happen. If we call north with 20 tiles left in the wall, we get to draw when there are 16, 12, … 0 tiles left in the wall, for 5 more draws. If we pass the call, we also end up with 5 draws. Calling a tile when the number of remaining tiles is divisible by 4 means that you don’t lose any draws if the game goes to exhaustive draw with no draw skipping calls, which is very likely here, given the incentives of 1st and 2nd place to fold. Most likely 3rd place will also end up folding or trying to play around the flush hand to hit tenpai.
The second factor is live tile reading. 2nd place cut 9s after they cut 2s, with 8s pon being called in between. Usually 2s is kept longer than 9s, so this reverse cut order suggests that 9s was kept as part of a larger shape, such as 899s, 799s, 779s, 889s, 6789s, 89s, or 79s. We see all the 9s, 3 8s, and 2 7s, allowing us to rule out most of these shapes. What remains is 779s (less likely), 6789s (less likely), 89s (less likely), and 79s (most likely). It is very likely that 2nd place is holding 7s in their hand, making the 3 tile wait even worse.
As expected, 2nd place had 79s, and drew 6s on the turn after 8s was called.
Conclusion: Call and cut 4s, because we don’t lose a draw, and to upgrade from 3 tiles (w/ 1 probably in 2nd place’s hand) to 4 tiles. The additional tsumo chance is worth the loss of being able to ron 3rd place.
In the east round of an east-south mahjong game, we play relatively straightforward, balancing the reward of winning our hand with the risk of dealing in to an opponent’s hand. On ladder, where only placement affects the payouts of the game, the final round can encourage some more polarized strategies. We may want to feed a player’s hand to protect a first place. We may want to hold back tiles to avoid feeding a competitor. We may need to meet a certain point requirement to escape 4th place, forcing us to build for value. Understanding each player’s incentives should influence our strategy.
The final round also has the most consequential decisions.
In this post, we’ll assume a normalized reward system of [2, 1, 0, -3] for 1st through 4th place. While a mangan win in East 1 moves our expected reward by around 1 point, it could be a swing from 4th (-3 pts) to 2nd place (-1 pt) for 4 pts in all last.
I want to share 3 of the most interesting South 4 decisions I’ve come across in my last 400 games of mahjong. Can you find the most optimal moves in the most important round of the game? I encourage readers to make their decision with reasoning before reading my analysis. For an additional challenge, come up with your gut answer (you only get 5 seconds + your time bank in a real game), and your thought out answer.
Problem 1
Tiles cut from the hand are white, and tiles that were cut upon being drawn are gray.
The number 9 in the center of the board shows how many tiles are left to be drawn in the round. On the last draw of the round, there will be 0 draws remaining.
Let’s start by ignoring the irrelevant players. 1st place is dealer in South 4 with a big lead, so they will simply fold and confirm 1st. 2nd place has a sizable lead over 3rd and 4th, with no incentive to take any risk with 2 draws left, so they will also fold. We can confirm from their last several safe discards from hand that they are choosing to fold.
We’re in 3rd place at 1-shanten, with a small lead over 4th. If we can hit tenpai within our final 2 draws, we can confirm 3rd place on exhaustive draw. 4th place has 3 draws, and can escape 4th by winning a hand, or hitting tenpai, while 3rd place misses out on tenpai.
Pystyle does not consider making calls from other players which is fine, since we do not expect to get fed by 2nd place, who is folding. We could potentially call pon on a tile 4th place cuts, but we’ll ignore this minor detail in our analysis.
My initial reaction to this problem was to cut 5s for maximum tile acceptance, but there is a tradeoff. If we cut 5s, we might feed 4th place a call into tenpai, which would cost us if they hit tenpai while we don’t. How do we know if this tradeoff is worth it?
Let’s try to make a read on how far 4th place is from tenpai. In row 2, they cut the 13m kanchan which was missing 2 tiles. Usually block cuts are done from 1-shanten or 2-shanten, but since the middle tiles 4p and 7m are in their discards, I would guess they were more likely 1-shanten. They cut 1s from their hand after. Since this was the last 1s, we can narrow down why they kept 1s in their hand. They could have done a slide - having 123s, and drawing 4s. They also could have upgraded or completed a shape. For upgrades, they could have 12s => draw 2s or 4s, or 13s => draw 3s or 4s. For block completions, they could have 122s or 133s => draw 2s or 3s. It seems like there are more scenarios where 4th place did not advance from 2-shanten to 1-shanten, or 1-shanten to tenpai.
And most importantly, they haven’t declared riichi. We would expect 4th place to declare riichi unless they had a yaku to be able to declare ron. Usually this would be pinfu or tanyao, but pinfu is impossible if they completed 122s or 133s by drawing 2s or 3s. We can also rule out completed yakuhai as a yaku, and seven pairs is unlikely because of how long the dead 1s was held.
I’ll give 4th place a 10% chance of being tenpai, a 65% chance of being 1-shanten, and a 25% chance of being 2-shanten.
If 4th place is 1-shanten, what is the chance that each tile feeds them into tenpai, costing us our position?
With 4 4p and 4 8p visible, a row 1 49p cut, and 1 7p visible, 57p will pretty much never feed 4th place a call. With 5s and 6s, we could estimate the feed chance by the dealin rate of these tiles vs a riichi. Presumably 4th place is 1-shanten with one incomplete block around 1s and one elsewhere, so this should be a decent estimate. Consulting a dealinrate chart, non suji 56 is around 21% dealinrate on Turn 16. 6s is one chance on one side, making it less likely to feed than 5s. We could make a lower bound estimate of its dealinrate to be around 16%.
Finally, let’s estimate 4th place’s chance of hitting tenpai with 3 draws left. If they have a 16 tile 1-shanten, they hit tenpai roughly 35% of the time according to pystyle.
With all of these numbers, we can come to an estimate of the chance we get 4th place. We’ll ignore the 2-shanten case for simplicity, and assume that neither us nor 4th place wins the hand before exhaustive draw. These assumptions will not affect the results much, since with 2 or 3 draws, it is very rare for a 1-shanten hand to win or a 2-shanten hand to hit tenpai. We’ll also see from the results that the difference between the decisions is large enough that we don’t need a more precise analysis.
P(we get 4th) ~= P(we are not tenpai) * [P(4th place is tenpai) + P(4th place is 1-shanten) * [P(4th place does not call our tile) * P(4th place gets tenpai by self draw) + P(4th place gets tenpai by calling our tile)]]
57p cut:
4th rate = (1 - .2094) * [.1 + .65 * .35] = 25.9%
5s cut:
4th rate = (1 - .2499) * [.1 + .65 * [(1-.21) * .35 + .21]] = 31.2%
6s cut:
4th rate = (1 - .2365) * [.1 + .65 * [(1-.16) * .35 + .16]] = 30.2%
Conclusion: we should cut 57p to avoid the chance we feed 4th place into tenpai. It’s not worth feeding 1-shanten => tenpai ~10-13% (16-21% feed * 65% 1-shanten) of the time for an additional 4% tenpai rate.
Problem 2
Normally I would wait on the 9p, which seems more likely to come out due to the two 8p visible. However, Flan shared a problem on discord from a mahjong book by Kawamura Akihiro, which made me rethink this conventional wisdom.
The author argues that the other terminals 9p and 9s are more likely to come out. The left player is likely to cut 9p and 9s if they draw them, because terminals are generally hard to use (though 9m is harder to use). However, there is the added benefit that they might cut 9p or 9s from their hand, whereas 9m is likely not in their hand. In summary, a tile like 9p can be discarded after being drawn, or from the hand. 9m is slightly more likely to be discarded after being drawn, but less likely to be discarded from the hand.
The author refers to an analysis where 9m is cut in the early game 413 times, and the rest of the 5 terminals 2566 times. For a specific terminal, this is 2566/5 = 513.2 times. This is a 24% relative increase in the probability that the player cuts the other terminal in the early game, a pretty large difference.
I have some questions about this analysis, which was not fully detailed. What cutoff turn was used to define early game? What percentage of the time did our left player cut each terminal from hand, vs after drawing it? What percentage of the time are we able to draw the tile ourselves? If a tile we want to call is more likely to be in an opponent’s hand, it would also be less live in the wall, which may counteract the benefit of getting more calls. However, I do think that the analysis presented mitigates this downside. In the analysis described above, having the tile in the left player's hand is strong enough to make up for both the increased chance that they draw the tile (if it's not in their hand, it's more live in the wall), and the increased chance that they cut the tile after drawing it. And this increased chance is a suprising 24%. It seems plausible that we would rather have the tile in the left player’s hand than in the wall.
Let’s go back to the original problem. Our left player looks unlikely to have either 1p or 9p, and will probably cut both. The player across from us probably does not have 9p, but might have 1p, which according to the book significantly increases the chances that they feed 1p in an early turn. The player on the right may have both tiles, but are probably slightly more likely to have 1p, since 2 8p being visible makes them more encouraged to toss 9p. They’re probably slightly more likely to cut 9p if they draw it, but this may be balanced by the higher chance 1p is in their hand and will get cut. And finally, we have the counteracting effect of 9p being more live in the wall, making it more likely for us to draw it.
If you believe the logic from the book, the answer to this problem is probably that we should wait on 1p. Because of the book’s vague description of it's data collection process, I’m not fully convinced, but for now, I’ll tentatively say we should wait on 1p. I would like to see a replication of the book's findings in the future.
Here are the hands from that round:
Problem 3
We have a honitsu hand that is tenpai, and we can escape 4th place by tsumo, or by ron on 2nd or 3rd place.
1st place is trying to feed our hand, since they can dealin to a 7 han hand and confirm 1st.
It looks like 2nd place has decided to fold, cutting a 1p from their hand, followed by 9m pair from their hand. Note that 2nd place has less of an incentive than 3rd place to fight. 2nd place can avoid 4th place by 100 pts if we mangan tsumo. Even if 2nd place folds, 3rd place might also fold allowing 2nd place to secure their position without taking any risk.
On the other hand, if 3rd place hits tenpai while 2nd place folds, they can steal 2nd place. 3rd place should be willing to take some risks for a chance at 2nd, keeping in mind the rewards of +1 for 2nd, +0 for 3rd, and -3 for 4th.
We have two options. We can call the north pair and go for furiten tsumo, or we can pass and go for tsumo or ron on 2nd / 3rd place. We probably won’t ron 2nd place, but 3rd place might cut north, or even 7s depending on the situation.
For example, on the last draw of the game if 2nd place had folded out, 3rd place should be willing to push up to a 25% dealin tile to go for 2nd place. 75% of the time, they would gain 1 pt, and 25% of the time they would lose 3 pts, for a net balance of 0 EV, making 25% the dealinrate threshold. North also seems decently safe, being a once cut honor tile if we pass this call. It’s possible 3rd place pushes north if they have a good wait tenpai, or are tenpai and we are close to exhaustive draw.
If we go for the furiten route, we would pon and cut 4s, giving a furiten wait of 4 tiles. North confirms our 4th han, so we don’t need the dora for points. We would upgrade from 3 to 4 outs, but we lose the ability to declare ron on 3rd place.
I think there are 2 factors that push this decision in favor of pon => cut 4s.
The first factor is the turn number. Normally, calling means you lose a draw, but this is not the case here, assuming no other calls happen. If we call north with 20 tiles left in the wall, we get to draw when there are 16, 12, … 0 tiles left in the wall, for 5 more draws. If we pass the call, we also end up with 5 draws. Calling a tile when the number of remaining tiles is divisible by 4 means that you don’t lose any draws if the game goes to exhaustive draw with no draw skipping calls, which is very likely here, given the incentives of 1st and 2nd place to fold. Most likely 3rd place will also end up folding or trying to play around the flush hand to hit tenpai.
The second factor is live tile reading. 2nd place cut 9s after they cut 2s, with 8s pon being called in between. Usually 2s is kept longer than 9s, so this reverse cut order suggests that 9s was kept as part of a larger shape, such as 899s, 799s, 779s, 889s, 6789s, 89s, or 79s. We see all the 9s, 3 8s, and 2 7s, allowing us to rule out most of these shapes. What remains is 779s (less likely), 6789s (less likely), 89s (less likely), and 79s (most likely). It is very likely that 2nd place is holding 7s in their hand, making the 3 tile wait even worse.
As expected, 2nd place had 79s, and drew 6s on the turn after 8s was called.
Conclusion: Call and cut 4s, because we don’t lose a draw, and to upgrade from 3 tiles (w/ 1 probably in 2nd place’s hand) to 4 tiles. The additional tsumo chance is worth the loss of being able to ron 3rd place.
Comments
Post a Comment